Sorcerous Solitaire

The sorcerer, in addition to being an evil old bastard, doesn't play fair. It is not possible to win the game as described, so you'll be sitting at that table for a very long time.

To see this, we first color the board as such:

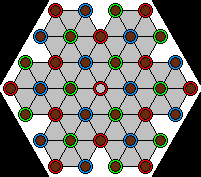
At the starting position, there are twelve pegs in positions of each colour. Each move will decrease by one the number of pegs in two of the colours, and increase by one the number of pegs in one of the colours. Since all three colours had an even number of pegs at the start, and since each move will change the number of pegs of each colour by one, the colours will shift back and forth between all being even-numbered and all being odd-numbered. There will never be a point where one colour is odd and the other two are even.
But that's what the winning position looks like: one peg of one colour, and zero pegs of the other two colours.